In Wikipedia we trust =))
The bit is a basic unit of information in information theory, computing, and digital communications. The name is a portmanteau of binary digit.
To resolve some real world problems, bit manipulation is simply a useful technique to optimize our code. So mastering it is never be redundant.
These following pack of expressions are useful in bit manipulations. Let's figure out.
XOR
x ^ 00- = x //00- is sequence of 0 only
x ^ 11- = ~x //11- is sequence of 1 only
x ^ x = 0
We have XOR table below:
| ^ | 0 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 0 |
Even with bit 0 or 1, we always get same result when do XOR with 0, reversed value when do with 1.
In case they are same bits, we will get 0 as result. So the third expression are correct.
AND
x & 00- = 0
x & 11- = x
x & x = x
These are not hard to figure out because 1 & 1 = 1, 0 & 1 = 0, 0 & 0 = 0
OR
x | 00- = x
x | 11- = 11-
x | x = x
In these expressions, we can think bit 1 is more powerful than bit 0, the result always get 1 if we see 1, only get 0 when both sides are 0.
Bit Right-Shifting
There are 2 types of right shift operators.
Arithmetic Shifting
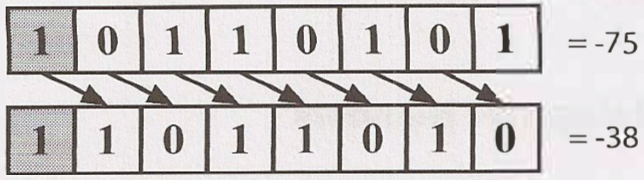
Logical Shifting
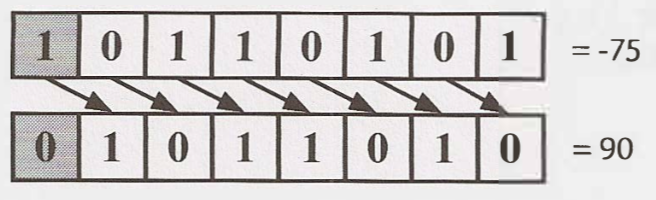
In Arithmetic right shift, we shift values to the right and fill the new bits with value of the sign bit, so it's equal to essentially be divided by $2^n$ when do shifting n bit.
12 >> 1 = 12 / 2 = 6
-12 >> 2 = -12 / 4 = -3
In Logical right shift, we shift the bits and put a 0 in the most significant bit (see image above - the sign bit is indicated with a gray background). So we will get 0 as result when shifting right all of bits.
In Swift programming language, with Signed-integers, they use Arithmetic Shifting, with Unsigned-Integers they use Logical Shifting. So depend on datatype we will get different result.
Talk is cheapppp =)), please check source code below for more details :)
func repeatedArithmeticShift(x: Int8, count: Int) -> Int8 {
var val = x
for _ in 0..<count {
val >>= 1
}
return val
}
func repeatedLogicalShift(x: UInt8, count: Int) -> UInt8 {
var val = x
for _ in 0..<count {
val >>= 1
}
return val
}
repeatedLogicalShift(x: 0b11111111, count: 1) //127
repeatedArithmeticShift(x: -0b1111111, count: 1) //64
//these numbers have same representation (11 111 111) :
// 256 as unsigned, -1 as signed
repeatedLogicalShift(x: 0b11111111, count: 10) //0
repeatedArithmeticShift(x: -0b1111111, count: 10) //-1
GET/SET/CLEAR/UPDATE i-th bit
To complete these tasks, we do
- Left shift
1i times to the left to create the mask (eg:00010000or11011111 - Apply mask to the numbers
- Get result
extension Int {
func getBit(at: UInt8) -> Bool {
return (self & (1 << at)) != 0
}
func setBit(at: UInt8) -> Int {
return self | (1 << at)
}
func clearBit(at: UInt8) -> Int {
let mask = ~(1 << at)
return self & mask
}
func updateBit(at: UInt8, val: Bool) -> Int {
let value = val ? 1 : 0
let mask = ~(1 << at)
return (self & mask) | (value << at)
}
}
...
...
Those group of peoples next to my table are using English for their conversations. They are 100 percent Vietnamese.
So to be globally, need to master English not Japanese =))
Thanks for reading.
Happy coding.