Fun with Prime Numbers

Wikipedia says:

A prime number (or a prime) is a natural number greater than 1 that cannot be formed by multiplying two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, 1 × 5 or 5 × 1, involve 5 itself. However, 6 is composite because it is the product of two numbers (2 × 3) that are both smaller than 6.

Therefore, to check if a number is prime, we need to check for it's divisibility on all numbers less that it, start from 2 through the square root of it.

extension Int {
    var isPrime: Bool {
        if self < 2 { return false }
        var x = 2
        while (x * x <= self) {
            if self % x == 0 { return false }
            x += 1
        }
        return true
    }
}

In episode 7 of Vietnamese version of The Brain gameshow, a young student was challenged to find a password to unlock a treasure. The password was hidden on a board of 1380 numbers with 5 in length. In those 1380 numbers, there were 7 prime numbers formed a polygons with only 2 diagonal lines that are perpendicular(90 degrees). The password is at the intersection of those 2 lines. See picture below

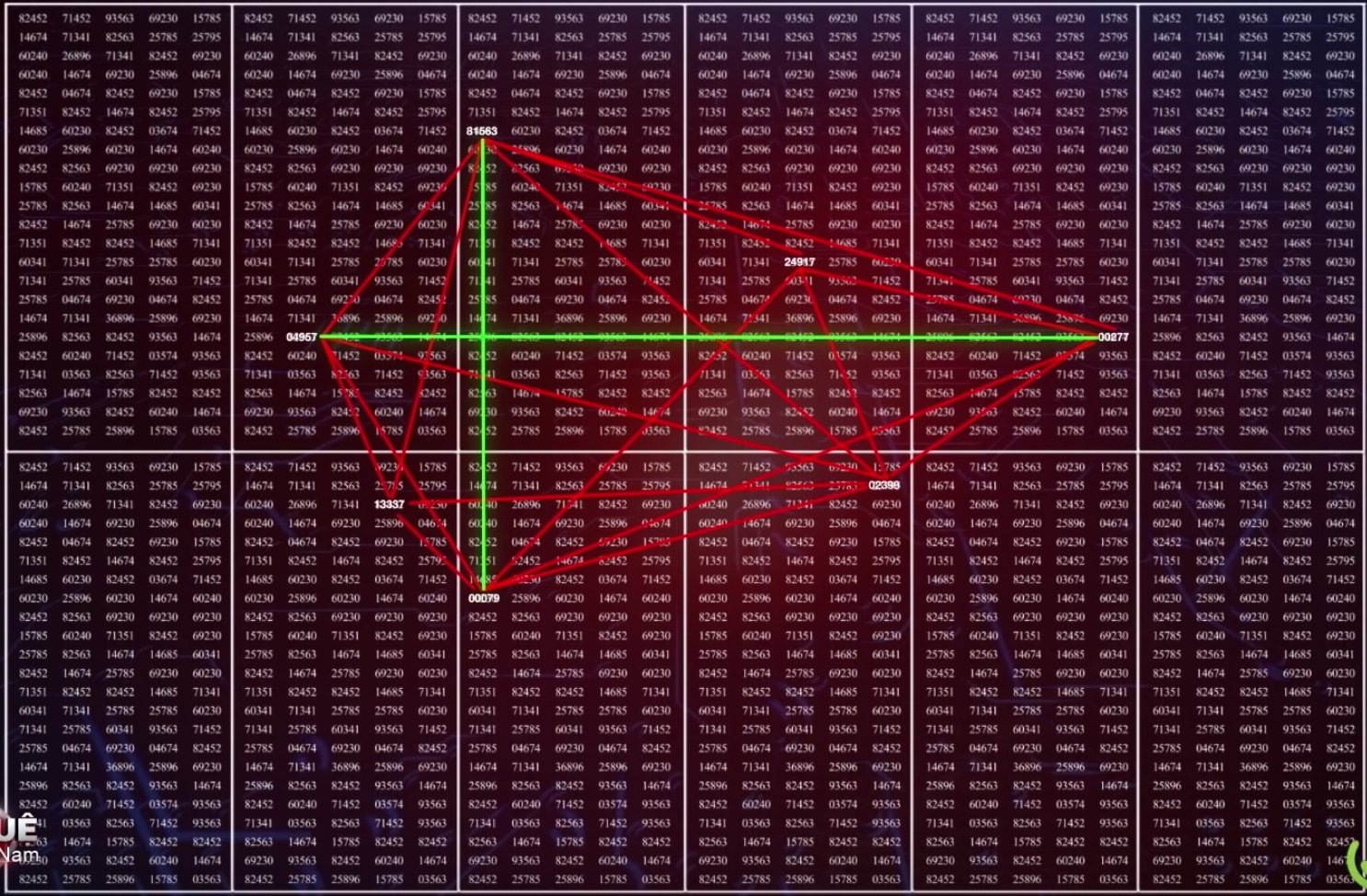
He solved the problem in 30 minutes. What a genius boy.

From my viewpoint as a software engineer, I'm trying to figure out the most efficient way to implement his brain to resolve this problem. :)

The only way to solve is to scan the 2D matrix and find 7 prime numbers. Then find the intersection of perpendicular diagonals. If we use the function isPrime above for every number, our algorithm with do duplicated works. How about pre-generate a set of prime numbers that are less than 100000

extension Int {
    var lowerPrimes: [Int] {
        var isPrimeArray = Array(repeating: true, count: self + 1)

        var currentPrime = 2
        while currentPrime <= Int(sqrt(Float(self))) {
            for i in stride(from: currentPrime * currentPrime, through: self, by: currentPrime) {
                isPrimeArray[i] = false
            }
            repeat {
                currentPrime += 1
            } while (isPrimeArray[currentPrime] == false && currentPrime < self + 1)
        }


        //display all result with list
        var result: [Int] = []

        for i in 2..<isPrimeArray.count {
            if isPrimeArray[i] {
                result.append(i)
            }
        }

        return result
    }
}

Let me describe a abit about function above. Start from currentPrime = 2, we mark all numbers greater than 2 * 2 that's divisible by 2 follow this formula: 4 + 2 * i. Then increase currentPrime till it's not appear on the mark list. Repeate previous step.
After done the process we will have list of primes.

Continue with our algorithm, with every number just take constant time to check isPrime. Space complexity here is O(n) - n is largest posible number of the board, and time complexity is O(p x q) - board's size.

func findPassword(_ board: [[Int]]) -> Int {
    let boardMax = board.reduce([], +).max()!
    let primes = Set(boardMax.lowerPrimes)
    
    var polygons: [(Int, Int)] = []
    
    for i in 0..<board.count {
        for j in 0..<board[0].count {
            if primes.contains(board[i][j]) { polygons.append((i,j)) }
        }
    }
    
    let sortedX = polygons.sorted { $0.0 < $1.0 }
    let sortedY = polygons.sorted { $0.1 < $1.1 }
    
    print(polygons)
    
    var x: Int = -1
    for i in 1..<sortedX.count {
        if sortedX[i].0 == sortedX[i-1].0 {
            x = sortedX[i].0
        }
    }
    
    var y: Int = -1
    for i in 1..<sortedY.count {
        if sortedY[i].1 == sortedY[i-1].1 {
            y = sortedY[i].1
        }
    }
    
    if x == -1 || y == -1 {
        return -1
    }
    
    return board[x][y]
}

And this is the game's board

func generateBoard() -> [[Int]] {
    var board = Array(repeating: Array(repeating: 4, count: 41), count: 47)
    
    //password
    board[20][14] = 17845
    
    //primes
    board[20][7] = 1489
    board[25][9] = 587
    board[14][11] = 3167
    board[3][14] = 2137
    board[33][14] = 823
    board[7][17] = 977
    board[20][21] = 9341
    
    return board
}

Summary, to have his brain we need to remember all prime numbers that are lower than 10000... HOW???

https://www.mathsisfun.com/numbers/prime-numbers-to-10k.html

Happy coding.